数据结构
string、hash、list、set、zset、bitmap、HyperLogLog、Bloom Filter(布隆过滤器)、stream
常用的前5种类型不做细究,来看看后面一个的结构及用法。
bitmap
在我们平时开发过程中,会有一些 bool 型数据需要存取,比如用户一年的签到记录,签了是 1,没签是 0,要记录 365 天。如果使用普通的 key/value,每个用户要记录 365 个,当用户上亿的时候,需要的存储空间是惊人的。 为了解决这个问题,Redis 提供了位图数据结构,这样每天的签到记录只占据一个位,365 天就是 365 个位,46 个字节 (一个稍长一点的字符串) 就可以完全容纳下,这就大大节约了存储空间。

位图不是特殊的数据结构,它的内容其实就是普通的字符串,也就是 byte 数组。我们可以使用普通的 get/set 直接获取和设置整个位图的内容,也可以使用位图操作 getbit/setbit 等将 byte 数组看成「位数组」来处理。
当我们要统计月活的时候,因为需要去重,需要使用 set 来记录所有活跃用户的 id,这非常浪费内存。这时就可以考虑使用位图来标记用户的活跃状态。每个用户会都在这个位图的一个确定位置上,0 表示不活跃,1 表示活跃。然后到月底 遍历一次位图就可以得到月度活跃用户数。不过这个方法也是有条件的,那就是 userid 是整数连续的,并且活跃占比较高,否则可能得不偿失。
基本使用
Redis 的位数组是自动扩展,如果设置了某个偏移位置超出了现有的内容范围,就会自动将位数组进行零扩充。
来了解几个命令:
- setbit key offset value 对 key 所储存的字符串值,设置或清除指定偏移量上的位(bit)。
- getbit key offset 对 key 所储存的字符串值,获取指定偏移量上的位(bit)。
- BITCOUNT key [start] [end] 计算给定字符串中,被设置为 1 的比特位的数量。
```
127.0.0.1:6379> setbit s 1 1
(integer) 0
127.0.0.1:6379> setbit s 2 1
(integer) 0
127.0.0.1:6379> setbit s 4 1
(integer) 0
127.0.0.1:6379> setbit s 9 1
(integer) 0
127.0.0.1:6379> setbit s 10 1
(integer) 0
127.0.0.1:6379> setbit s 13 1
(integer) 0
127.0.0.1:6379> setbit s 15 1
(integer) 0
127.0.0.1:6379> get s
“he” #01101000 01100101
127.0.0.1:6379> getbit s 1 (integer) 1 127.0.0.1:6379> BITCOUNT s (integer) 7
## HyperLogLog
### 概念
先来了解下基数计数,基数计数是用于统计一个集合中不重复的元素个数,比如统计页面的UV或者在线的用户数、注册IP数等。
你会如何实现?简单的做法就是记录集合中的所有不重复的集合S,新来元素x,首先判断x是不是在S中,若不再,集合添加x,反之不记录。常用的数据结构SET就可以实现。
但是存在问题,数据量越来越大,会造成什么问题?
- 统计的数据量变大时,相应的存储内存会线性增长;
- 当集合S越大时,判断x元素是否在集合S中的查询的成本会越来越大;
常用的基数计数有三种:B+树、bitmap、概率算法。
- B+树。插入、查找效率比较高。但是没有解决内存空间的问题。
- bitmap。基数计数将每一个元素对应到bit数组的其中一位,比如bit数组10010101,代表[1,4,6,8 ]。新加入的元素只需要已有的bit数组会让新加入的元素进行按位或计算。此种方式大大减少内存,如果存储1亿数据的话,大概只需要10000000000/8/1024=12M的内存。
相比B+树节省很多空间。但某些大数据场景,如果有10000个对象有1亿数据,则需要120G内存,特定场景下内存的消耗还是蛮大的。
- 概率算法,概率算法是通过牺牲准确率来换取空间,对于不要求绝对准确率的场景下,概率算法是一种不错的选择,因为概率算法不直接存储数据集合本身,通过一定的概率统计方法预估基数值,同时保证误差在一定范围内,这种方式可以大大减少
内存。HyperLogLog就是概率算法的一种实现。
### 原理
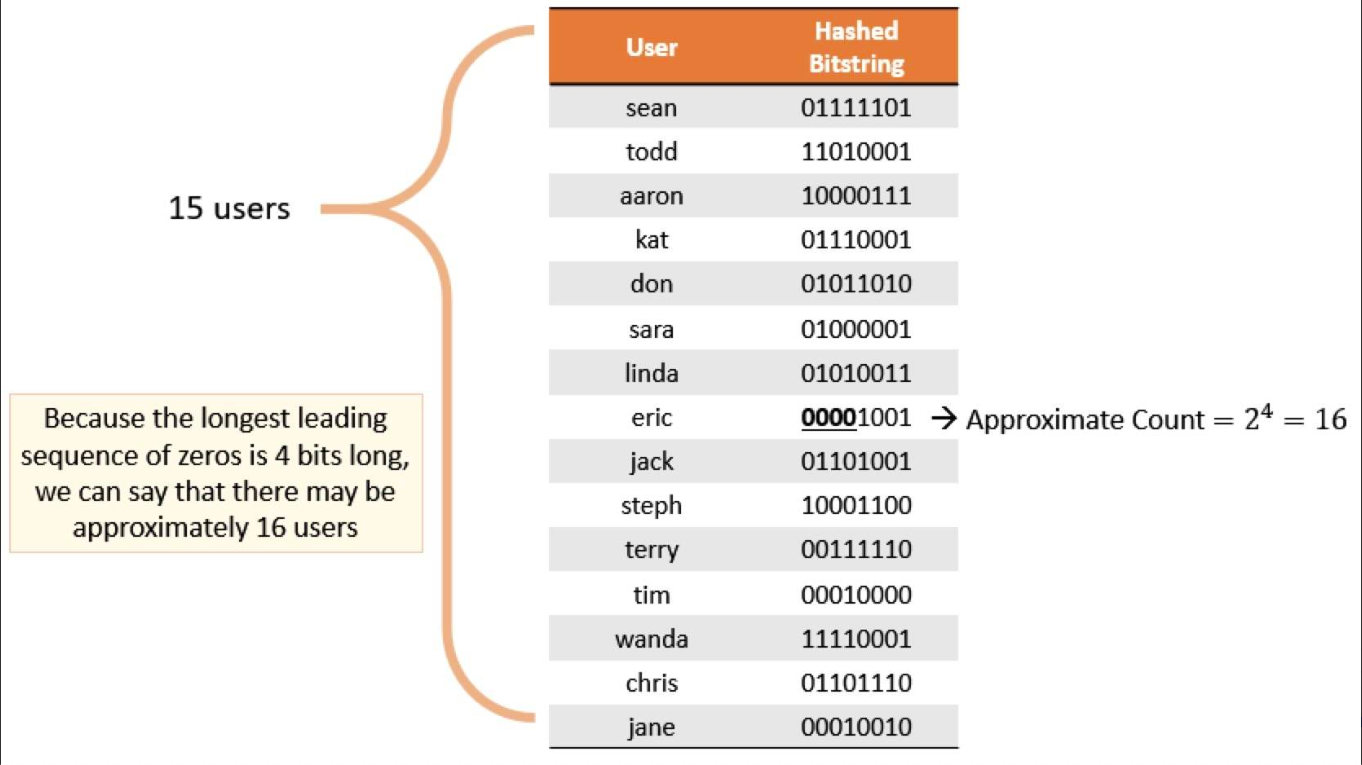
HyperLogLog原理思路是通过给定n个的元素集合,记录集合中数字的比特串第一个1出现位置的做大值k,也可以理解为统计二进制低位连续为零的最大个数。通过k值可以估算集合中不重复原色的数量m,m近似等于2^k。
下图来源于网络,通过给定一定数量的用户User,通过Hash得到一串Bitstring,记录其中最大连续零位的计数为4,User的不重复个数为 2 ^ 4 = 16.
### redis用法
主要涉及三个命令
- pfadd 增加一个元素到key中
- pfcount 统计key中不重复元素的个数
- Pfmerge 合并多个Key中的元素
pfadd 和 pfcount,根据字面意义很好理解,一个是增加计数,一个是获取计数。pfadd 用法和 set 集合的 sadd 是一样的,来一个用户 ID,就将用户 ID 塞进去就是。pfcount 和 scard 用法是一样的,直接获取计数值。
> pfmerge 适合什么场合用?
HyperLogLog 除了上面的 pfadd 和 pfcount 之外,还提供了第三个指令 pfmerge,用于将多个 pf 计数值累加在一起形成一个新的 pf 值。
比如在网站中我们有两个内容差不多的页面,运营说需要这两个页面的数据进行合并。其中页面的 UV 访问量也需要合并,那这个时候 pfmerge 就可以派上用场了
### 注意事项
HyperLogLog 这个数据结构不是免费的,不是说使用这个数据结构要花钱,它需要占据一定 12k 的存储空间,所以它不适合统计单个用户相关的数据。如果你的用户上亿,可以算算,这个空间成本是非常惊人的。但是相比 set 存储方案,HyperLogLog 所使用的空间那真是可以使用千斤对比四两来形容了。
不过你也不必过于担心,因为 Redis 对 HyperLogLog 的存储进行了优化,在计数比较小时,它的存储空间采用稀疏矩阵存储,空间占用很小,仅仅在计数慢慢变大,稀疏矩阵占用空间渐渐超过了阈值时才会一次性转变成稠密矩阵,才会占用 12k 的空间。
> 思考:如果你负责开发维护一个大型的网站,有一天老板找产品经理要网站每个网页每天的 UV 数据,然后让你来开发这个统计模块,你会如何实现?
其实老板需要的数据又不需要太精确,105w 和 106w 这两个数字对于老板们来说并没有多大区别,使用HyperLogLog轻松实现。
## 布隆过滤器
使用 HyperLogLog 数据结构来进行估数,它非常有价值,可以解决很多精确度不高的统计需求。
但是如果我们想知道某一个值是不是已经在 HyperLogLog 结构里面了,它就无能为力了,它只提供了 pfadd 和 pfcount 方法,没有提供 pfcontains 这种方法。
讲个使用场景,比如我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的?
你会想到服务器记录了用户看过的所有历史记录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那些已经存在的记录。问题是当用户量很大,每个用户看过的新闻又很多的情况下,这种方式,推荐系统的去重工作在性能上跟的上么?

实际上,如果历史记录存储在关系数据库里,去重就需要频繁地对数据库进行 exists 查询,当系统并发量很高时,数据库是很难扛住压力的。
### 布隆过滤器是什么?
布隆过滤器可以理解为一个不怎么精确的 set 结构,当你使用它的 contains 方法判断某个对象是否存在时,它可能会误判。但是布隆过滤器也不是特别不精确,只要参数设置的合理,它的精确度可以控制的相对足够精确,只会有小小的误判概率。
**当布隆过滤器说某个值存在时,这个值可能不存在;当它说不存在时,那就肯定不存在。** 打个比方,当它说不认识你时,肯定就不认识;当它说见过你时,可能根本就没见过面,不过因为你的脸跟它认识的人中某脸比较相似 (某些熟脸的系数组合),所
以误判以前见过你。
套在上面的使用场景中,布隆过滤器能准确过滤掉那些已经看过的内容,那些没有看过的新内容,它也会过滤掉极小一部分 (误判),但是绝大多数新内容它都能准确识别。这样就可以完全保证推荐给用户的内容都是无重复的。
### 布隆过滤器基本使用
布隆过滤器有二个基本指令,bf.add 添加元素,bf.exists 查询元素是否存在,它的用法和 set 集合的 sadd 和 sismember 差不多。注意 bf.add 只能一次添加一个元素,如果想要一次添加多个,就需要用到 bf.madd 指令。
同样如果需要一次查询多个元素是否存在,就需要用到 bf.mexists 指令。
### 布隆过滤器的原理
每个布隆过滤器对应到 Redis 的数据结构里面就是一个大型的位数组和几个不一样的无偏 hash 函数。所谓无偏就是能够把元素的 hash 值算得比较均匀。
向布隆过滤器中添加 key 时,会使用多个 hash 函数对 key 进行 hash 算得一个整数索引值然后对位数组长度进行取模运算得到一个位置,每个 hash 函数都会算得一个不同的位置。再把位数组的这几个位置都置为 1 就完成了 add 操作。
向布隆过滤器询问 key 是否存在时,跟 add 一样,也会把 hash 的几个位置都算出来,看看位数组中这几个位置是否都为 1,只要有一个位为 0,那么说明布隆过滤器中这个 key 不存在。如果都是 1,这并不能说明这个 key 就一定存在,只是
极有可能存在,因为这些位被置为 1 可能是因为其它的 key 存在所致。如果这个位数组比较稀疏,判断正确的概率就会很大,如果这个位数组比较拥挤,判断正确的概率就会降低。具体的概率计算公式比较复杂,感兴趣可以阅读扩展阅读,非常烧脑
,不建议读者细看。
使用时不要让实际元素远大于初始化大小,当实际元素开始超出初始化大小时,应该对布隆过滤器进行重建,重新分配一个 size 更大的过滤器,再将所有的历史元素批量 add 进去 (这就要求我们在其它的存储器中记录所有的历史元素)。因为
error_rate 不会因为数量超出就急剧增加,这就给我们重建过滤器提供了较为宽松的时间
### 空间占用估计
布隆过滤器的空间占用有一个简单的计算公式,但是推导比较繁琐,这里就省去推导过程了,直接引出计算公式。
布隆过滤器有两个参数,第一个是预计元素的数量 n,第二个是错误率 f。公式根据这两个输入得到两个输出,第一个输出是位数组的长度 l,也就是需要的存储空间大小 (bit),第二个输出是 hash 函数的最佳数量 k。hash 函数的数量也会直接
影响到错误率,最佳的数量会有最低的错误率。
k=0.7*(l/n) # 约等于
f=0.6185^(l/n) # ^ 表示次方计算,也就是 math.pow
从公式中可以看出
位数组相对越长 (l/n),错误率 f 越低,这个和直观上理解是一致的
位数组相对越长 (l/n),hash 函数需要的最佳数量也越多,影响计算效率
当一个元素平均需要 1 个字节 (8bit) 的指纹空间时 (l/n=8),错误率大约为 2%
错误率为 10%,一个元素需要的平均指纹空间为 4.792 个 bit,大约为 5bit
错误率为 1%,一个元素需要的平均指纹空间为 9.585 个 bit,大约为 10bit
错误率为 0.1%,一个元素需要的平均指纹空间为 14.377 个 bit,大约为 15bit
你也许会想,如果一个元素需要占据 15 个 bit,那相对 set 集合的空间优势是不是就没有那么明显了?这里需要明确的是,set 中会存储每个元素的内容,而布隆过滤器仅仅存储元素的指纹。元素的内容大小就是字符串的长度,它一般会有多个
字节,甚至是几十个上百个字节,每个元素本身还需要一个指针被 set 集合来引用,这个指针又会占去 4 个字节或 8 个字节,取决于系统是 32bit 还是 64bit。而指纹空间只有接近 2 个字节,所以布隆过滤器的空间优势还是非常明显的。
### 实际元素超出时,误判率会怎样变化
当实际元素超出预计元素时,错误率会有多大变化,它会急剧上升么,还是平缓地上升,这就需要另外一个公式,引入参数 t 表示实际元素和预计元素的倍数 t
f=(1-0.5^t)^k # 极限近似,k 是 hash 函数的最佳数量 ``` 当 t 增大时,错误率,f 也会跟着增大,分别选择错误率为 10%,1%,0.1% 的 k 值,画出它的曲线进行直观观察
从这个图中可以看出曲线还是比较陡峭的
错误率为 10% 时,倍数比为 2 时,错误率就会升至接近 40%,这个就比较危险了
错误率为 1% 时,倍数比为 2 时,错误率升至 15%,也挺可怕的
错误率为 0.1%,倍数比为 2 时,错误率升至 5%,也比较悬了