https://www.cnblogs.com/onepixel/p/7674659.html
https://zhuanlan.zhihu.com/p/41923298
算法
复杂度分析
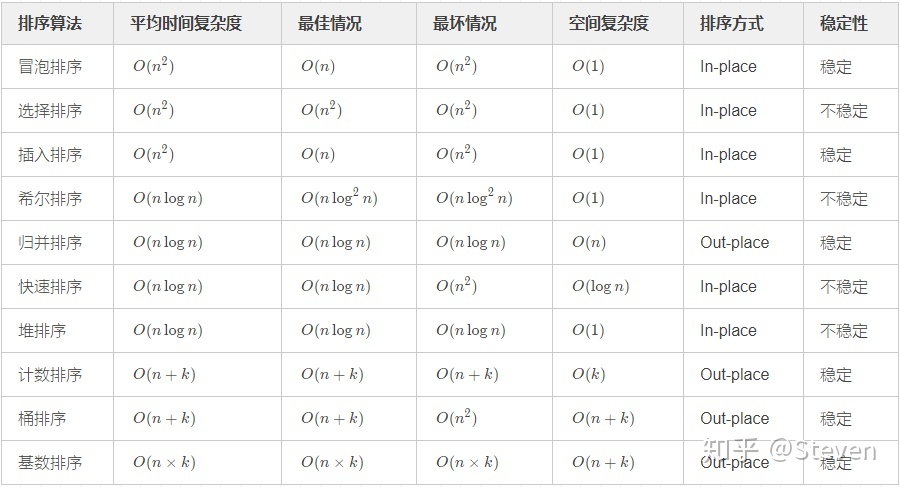
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机
冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述:
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
演示:
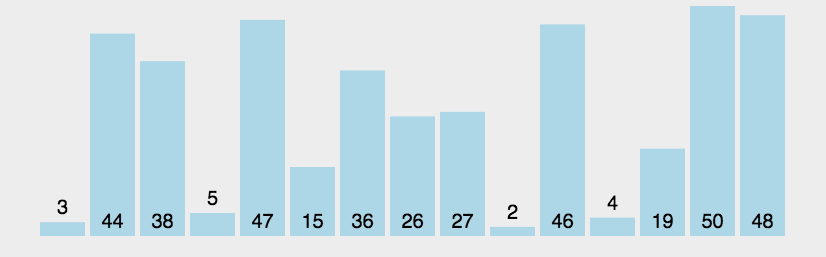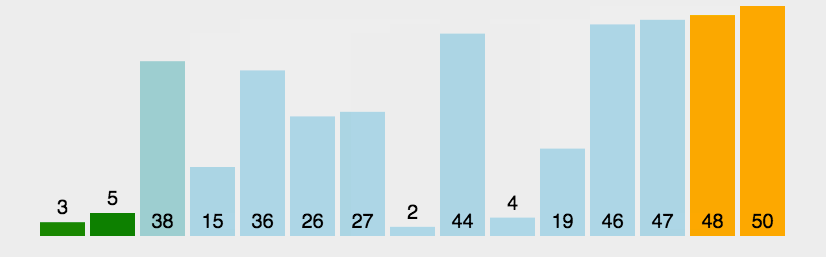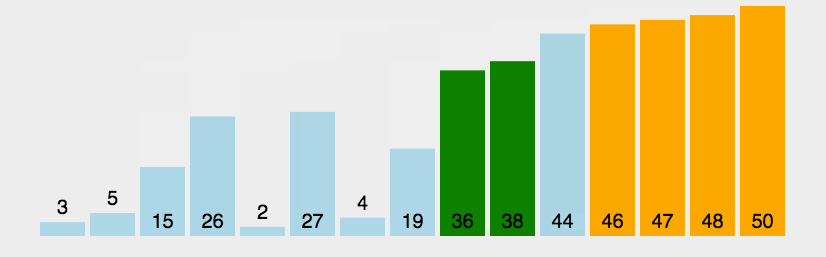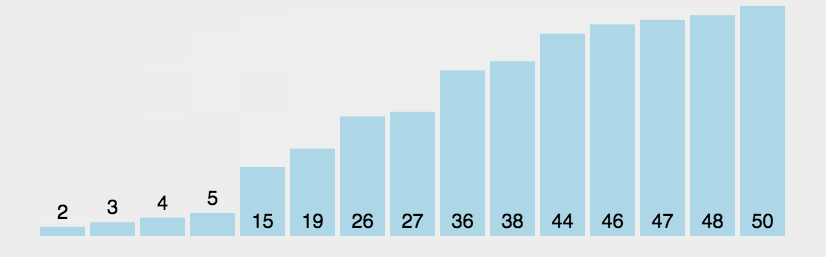
代码:
/**冒泡法排序
* @param array $data
* @return array
* @throws \Exception
*/
public function maopao( array $data ){
if( empty($data) )
throw new \Exception('array cannot null');
$count = count($data);
for ($i=0;$i<$count-1;$i++){
$swaped = 0;
for($j=0;$j<$count-$i-1;$j++){
if($data[$j]>$data[$j+1]){
[$data[$j+1],$data[$j]] = [ $data[$j] , $data[$j+1] ]; //php7 中list方括号写法
$swaped = 1;
}
}
//优化冒泡排序:某一趟没有交换元素,说明已经是正序排列,此时无需继续遍历,直接返回结果
//对于一个已经有序的数组,算法完成第一次循环后就会返回。实际上只发生了 N - 1次比较,所以最好的情况下,该算法复杂度是O(N)
if($swaped==0){
break;
}
}
return $data;
}
时间复杂度
若文件的初始状态是正序的,一趟扫描即可完成排序。所需的关键字比较次数 和记录移动次数 均达到最小值:Cmin = n-1, Mmin = 0 。
所以,冒泡排序最好的时间复杂度为 O(n)。
若初始文件是反序的,需要进行 n-1 趟排序。每趟排序要进行 n-i 次关键字的比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下,比较和移动次数均达到最大值:
C max = n(n-1)/2 = O(n^2)
冒泡排序的最坏时间复杂度为 O(n^2) 。
综上,因此冒泡排序总的平均时间复杂度为 O(n^2) 。
选择排序
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
- 初始状态:无序区为R[1..n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
演示:
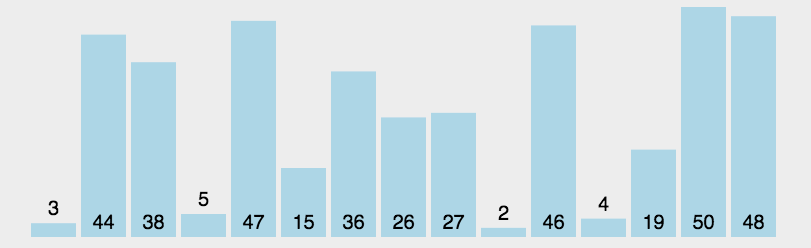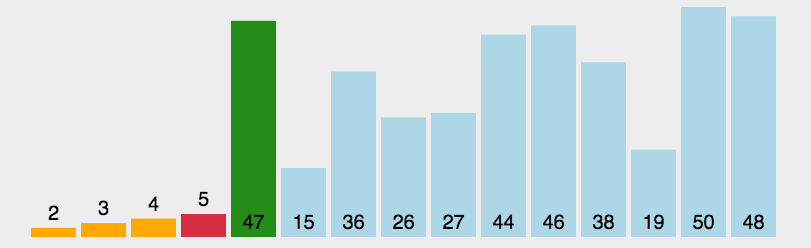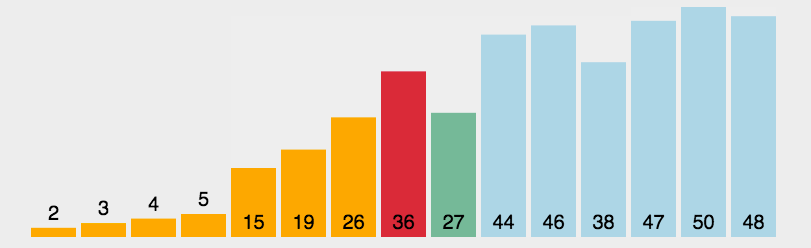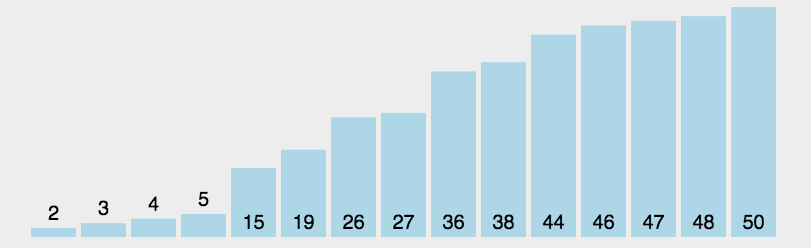
代码:
/**选择法排序
* @param array $data
* @return array
* @throws \Exception
*/
public function xuanze(array $data ){
if( empty($data) )
throw new \Exception('array cannot null');
$count = count($data);
for($i=0;$i<$count;$i++){
$min = $i;
for ($j=$i+1;$j<$count;$j++){
if($data[$i]>$data[$j]){
$min =$j;
}
}
[$data[$i],$data[$min]] = [$data[$min],$data[$i]];
}
return $data;
}
插入排序
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
演示
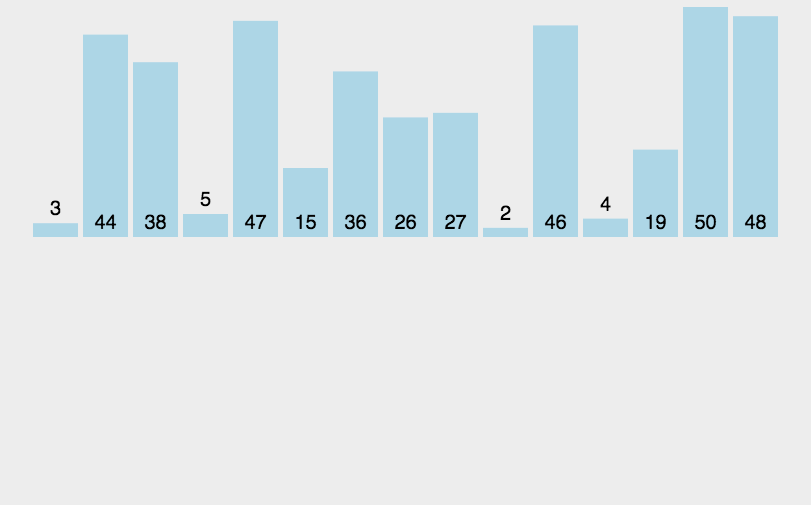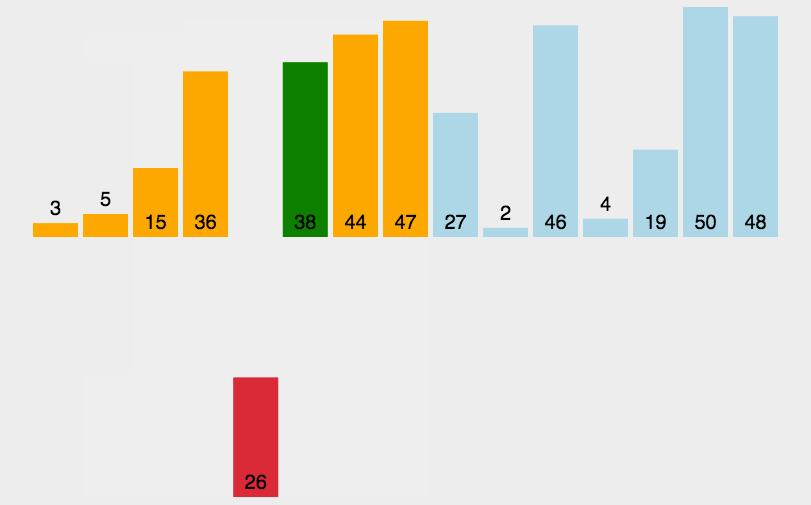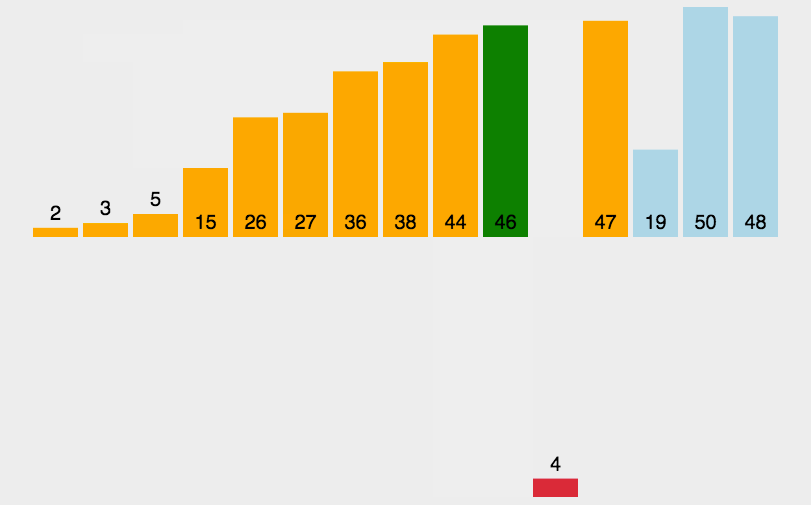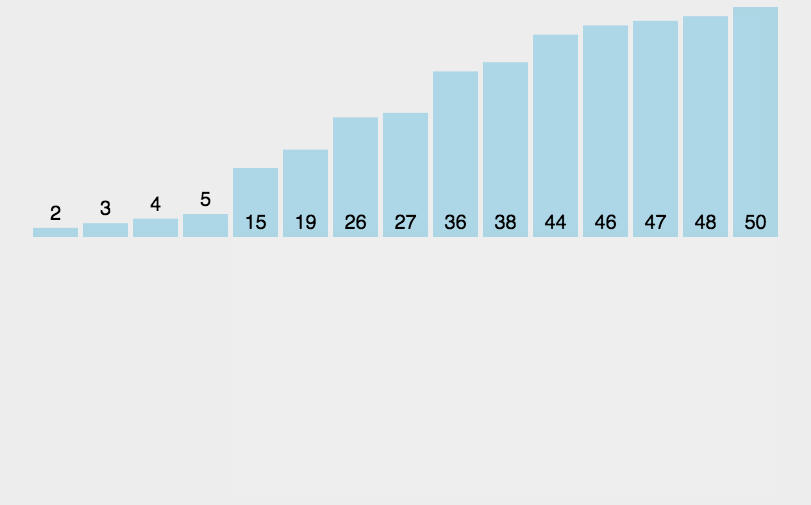
代码
/**
* @param array $data
* @return array
* @throws \Exception
*/
public function charu( array $data ){
if( empty($data) )
throw new \Exception('array cannot null');
$count = count($data);
for ($i=2;$i<$count;$i++){
$preIndex = $i;
$current = $data[$i];
for($j=$i-1;$j>=0;$j--){
if( $data[$j]>$current ){
$data[$j+1] = $data[$j];
$preIndex = $j;
}
}
$data[$preIndex] = $current;
}
return $data;
}
希尔排序
快速排序
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了
一趟快速排序的算法是:
1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
3)从j开始向前搜索,即由后开始向前搜索(j–),找到第一个小于key的值A[j],将A[j]和A[i]的值交换;
4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]和A[j]的值交换;
5)重复第3、4步,直到i=j; (3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。找到符合条件的值,进行交换的时候i, j指针位置不变。 另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
图示:
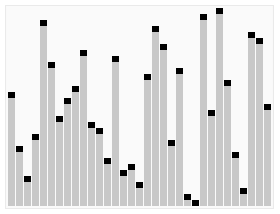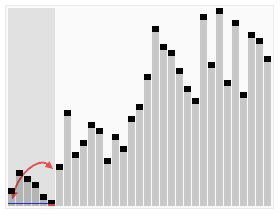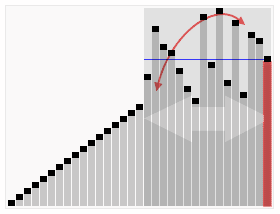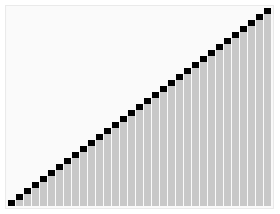
<?php
/**
* @param array $data
* @param int|null $start
* @param int|null $end
* @return array
*/
public function quickSort( array &$data,int $start=null,int $end=null ){
$start = $start??0;
$len = count($data);
$end = $end??($len-1);
$pivot = $data[$start]; //基准项
$j=$end;
$i=$start;
while($i<$j){
for (;$j>$i;$j--){
if($data[$j]<$pivot){
[$data[$i],$data[$j]] = [$data[$j],$data[$i]];
break;
}
}
for (;$i<$j;$i++){
if($data[$i]>$pivot){
[$data[$i],$data[$j]] = [$data[$j],$data[$i]];
break;
}
}
}
if( $start<$i-1 )
$this->quickSort($data,$start,$i-1);
if( $j+1<$end )
$this->quickSort($data,$j+1,$end);
return $data;
}
//优化版本
public function quickSort2($arr)
{
// 判断是否需要继续
if (count($arr) <= 1) {
return $arr;
}
$middle = $arr[0]; // 中间值
$left = array(); // 小于中间值
$right = array();// 大于中间值
// 循环比较
for ($i=1; $i < count($arr); $i++) {
if ($middle < $arr[$i]) {
// 大于中间值
$right[] = $arr[$i];
} else {
// 小于中间值
$left[] = $arr[$i];
}
}
// 递归排序两边
$left = $this->quick_sort($left);
$right = $this->quick_sort($right);
// 合并排序后的数据,别忘了合并中间值
return array_merge($left, array($middle), $right);
}
平均时间复杂度 nlogn