树

树结构是天然的组织结构，如计算机中的文件夹，mysql的存贮结构。

使用树结构存储后，出奇高效

分布：

二分搜索树
平衡二叉树：AVL；红黑树
堆；并查集
线段树；Tire（字典树，前缀树）

二叉树

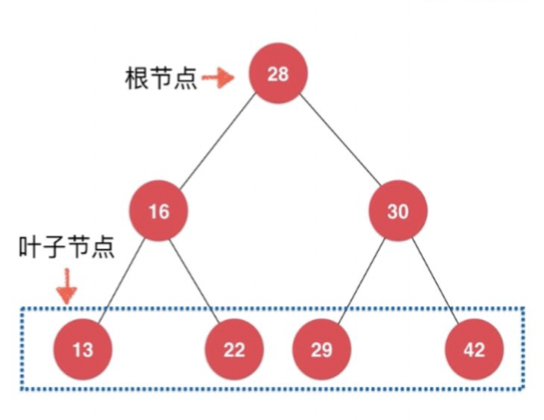
和链表一样，动态的数据结构
二叉树具有唯一根节点
二叉树每个节点最多两个孩子
每个节点最多一个父亲
二叉树具有天然递归结构
每个节点的左子树也是二叉树
每个节点的右子树也是二叉树
二叉树不一定是’满’的（一个节点也是二叉树，空也是）

Class Node{
    E e;
    Node left;
    Node right;
}

二叉树（多叉树）

二分搜索树

二分搜索树也是二叉树
二分搜索树的每个节点的值：
- 大于其左子树的所有节点的值
- 小于其右子树的所有节点的值
每个子树也是二分搜索树

添加新元素

二分搜索树不包含重复元素，如果想包含重复元素的话，只需定义：左子树小于等于节点；或者右子树大于等于节点。（注意数组链表支持重复元素）

二分搜索树添加元素的非递归写法和链表很像。

遍历

遍历类型：前序遍历、中序遍历、后序遍历（递归、队列、栈）、层序遍历

层序遍历：

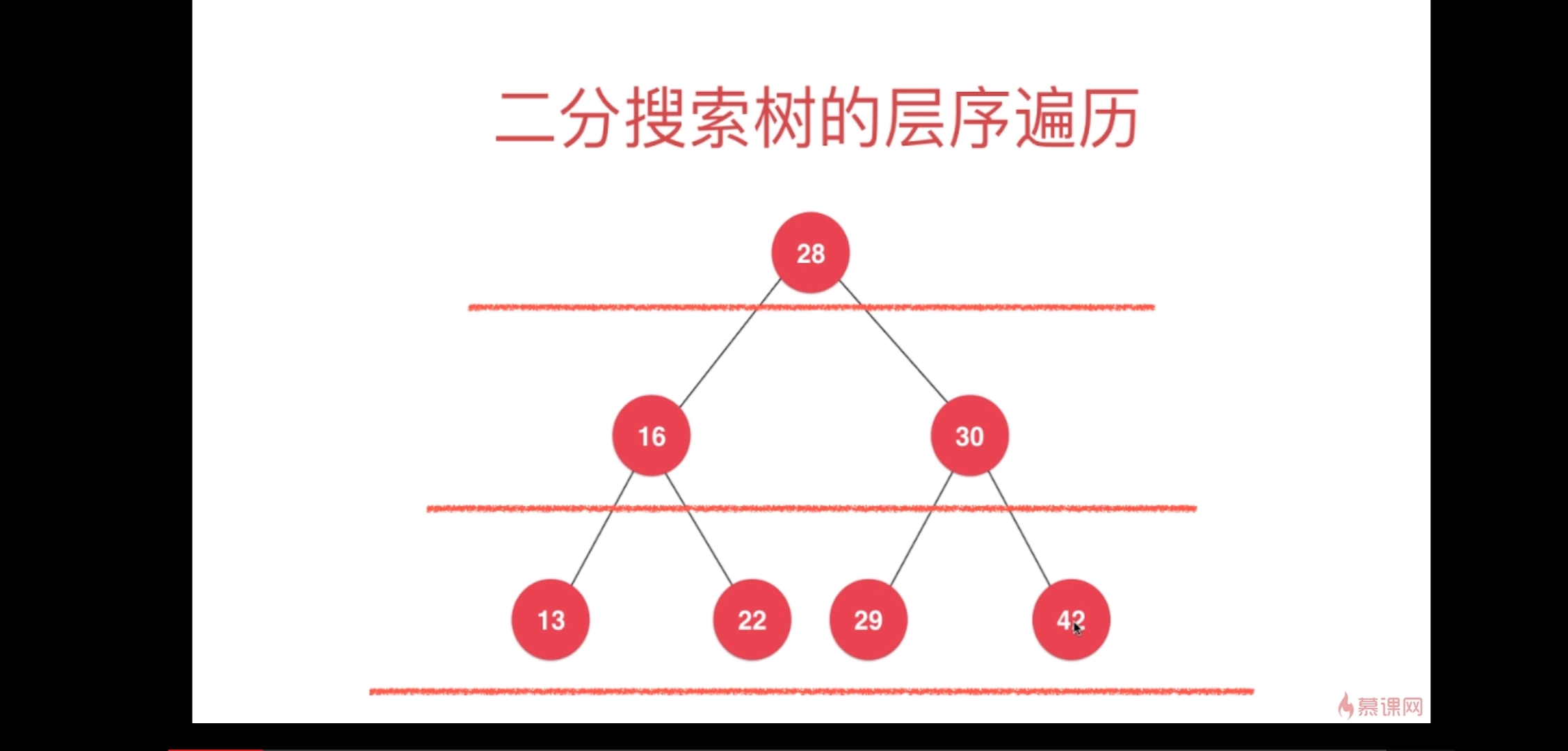
栈实现示意图：

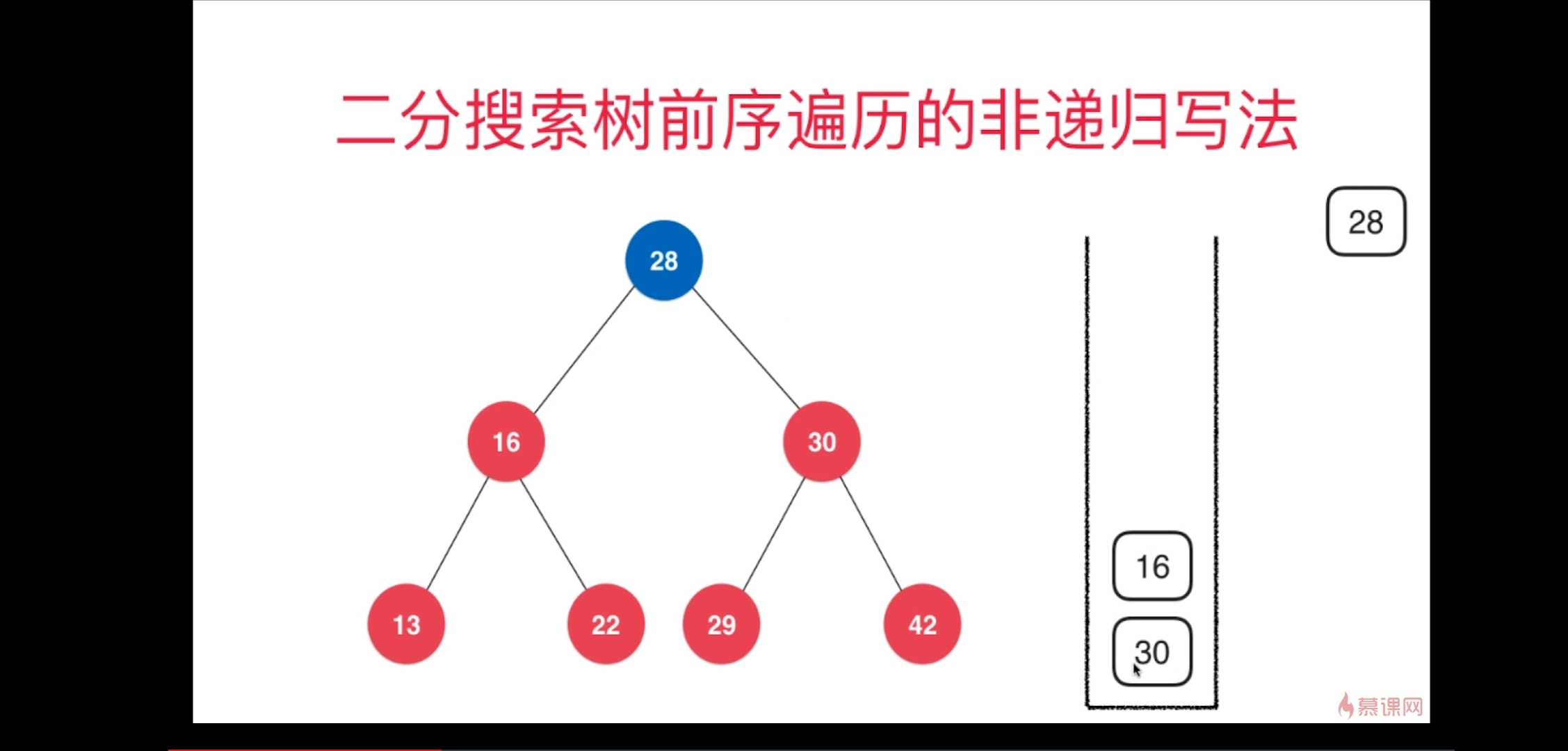
二分搜索树的非递归实现比递归实现复杂很多；

中序遍历和后序遍历的非递归实现更复杂；

中序遍历和后序遍历的非递归实现，实际运用不广；

删除操作

删除最小节点和最大节点相对来说是容易的

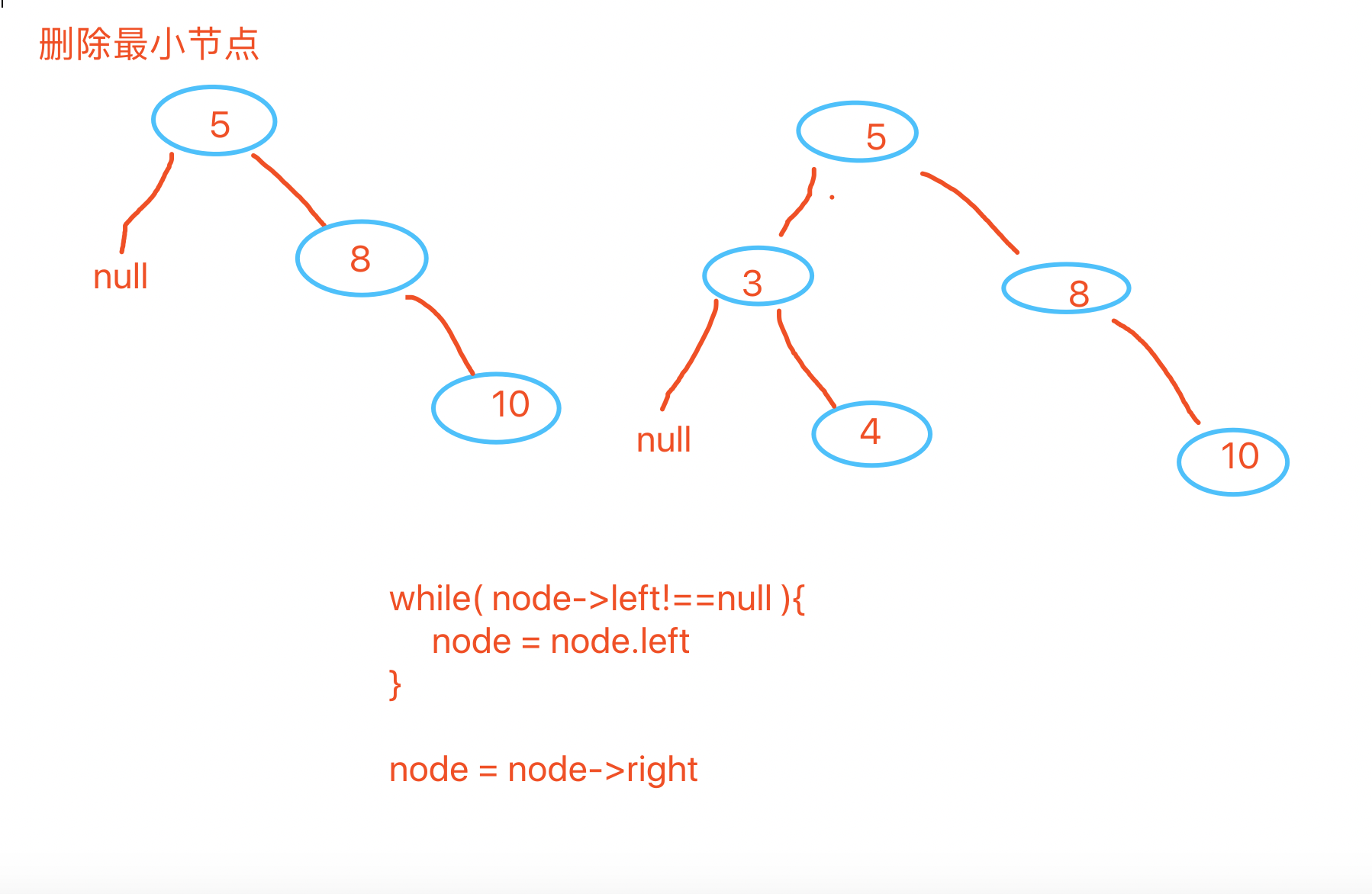
删除任意元素，需要考虑多种情况。

删除节点右边有孩子：

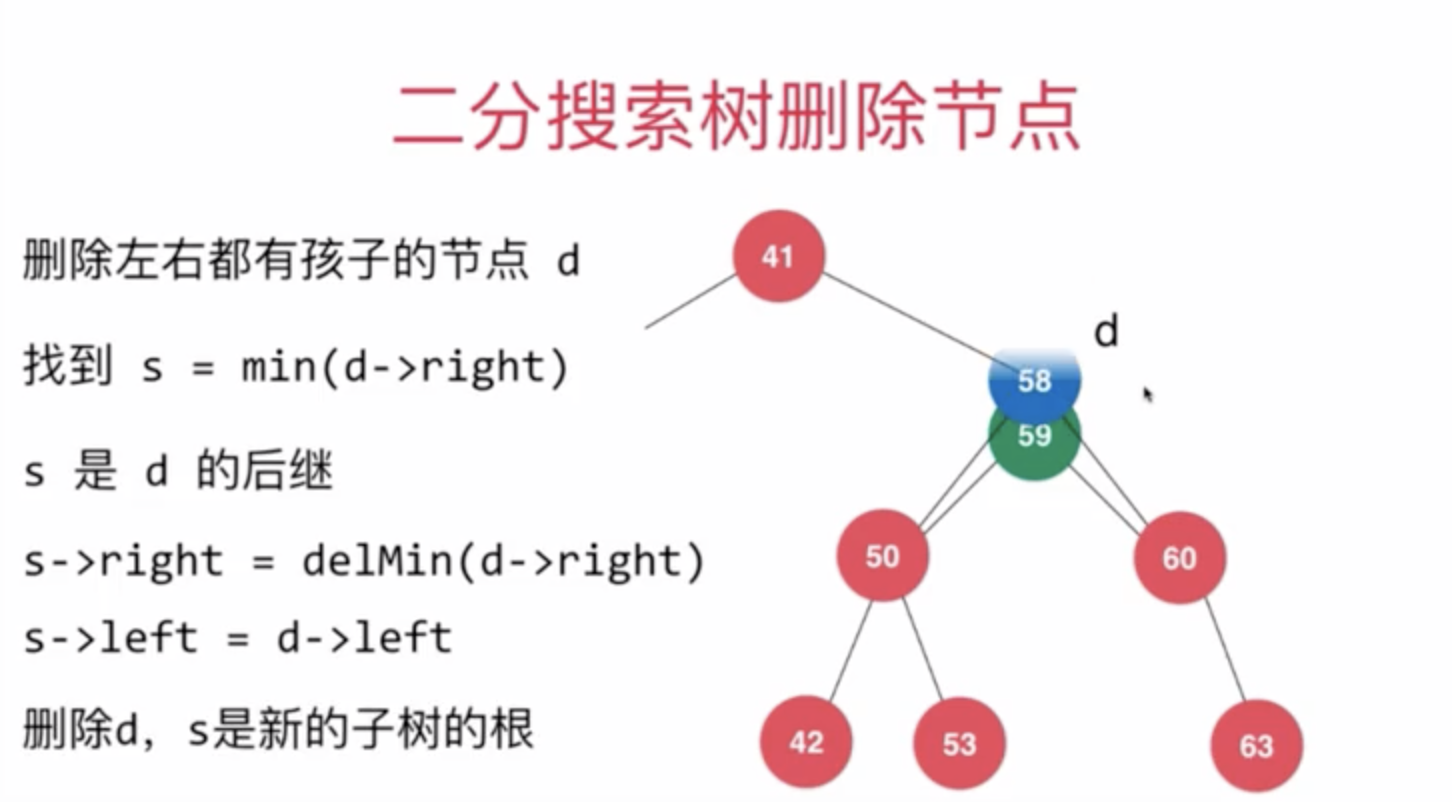
删除节点左边有孩子，右边无孩子：

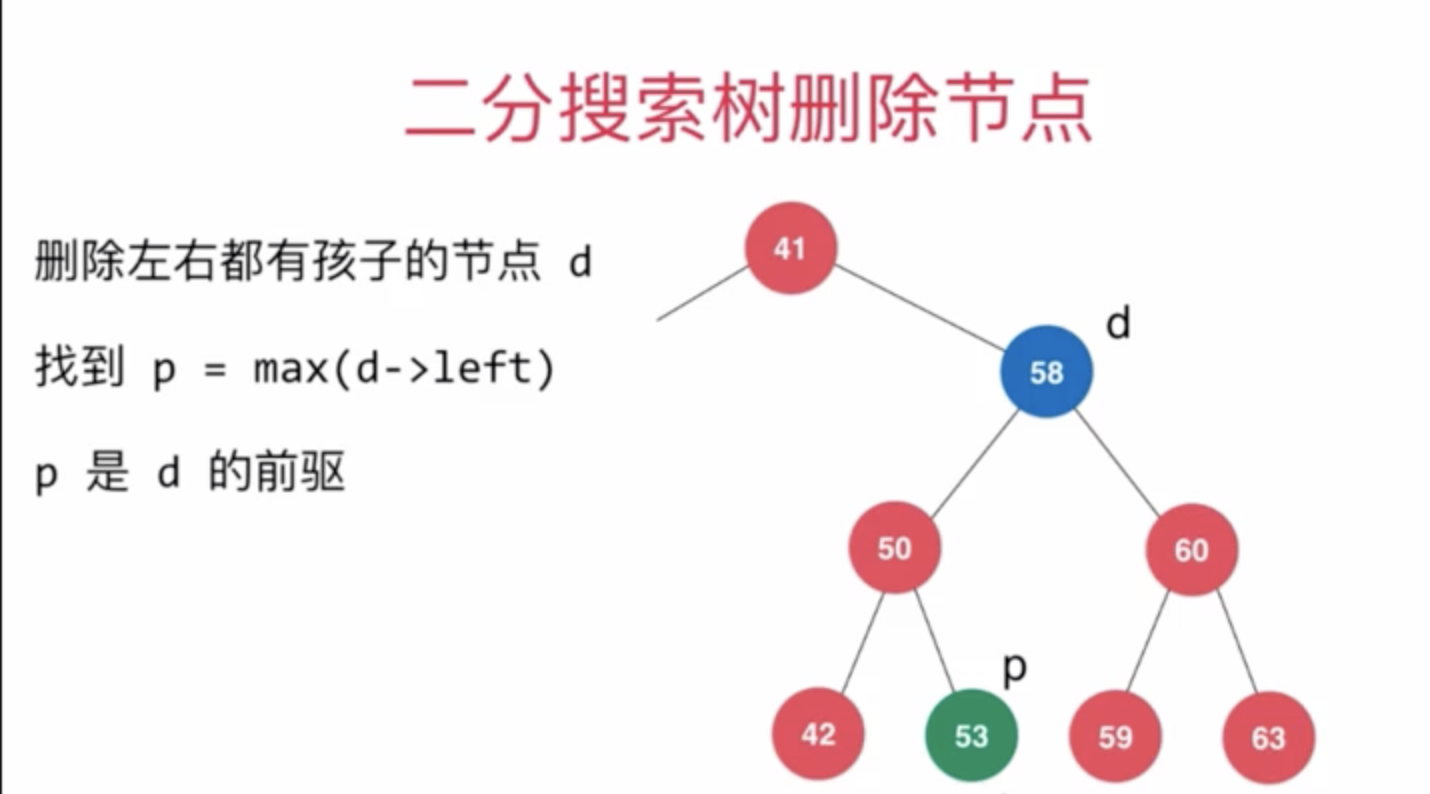
二分搜索树操作代码 ```php <?php

/**二分搜索树操作

Class TreeBinarySearch
@package app\models */ class TreeBinarySearch { public $val = null; public $left = null; public $right = null; public $size=0;

public function __construct($value=null){ $this->val = $value; }

/**添加元素
- @param $value
- @return TreeBinarySearch */ public function add( $value ){ $node = $this; return $this->add2($node,$value); }
public function selectBinary( $node, $value ){
```
 if($node==null)
     return false;

 if( $node->val == $value ){
     return $node;
 }

 if( $node->val > $value ){
     return  $this->selectBinary($node->left,$value);
 }else{
     return  $this->selectBinary($node->right,$value);
 }
```
}

/**查询
- @param string $type ‘pre’前序遍历，’in’中序遍历，’last’后序遍历 */ public function select( $value=null,$type=’pre’ ){ if($value) return $this->selectBinary($this,$value);
  
  switch ( $type ){ case ‘pre’: return $this->selectPreorderByStack($this); break; case ‘in’: return $this->selectInorder($this); //中序结果是顺序结构 break; case ‘last’: return $this->selectLastorder($this); //后序遍历应用：未二分搜索树释放内存 break; } }
/**
- 查询最小值 */ public function selectMin( $node ){ if( $node->left != null ){ $this->selectMin($node->left); }
  
  return $node;
}

/**
- 查询最大值 */ public function selectMax( $node ){ if( $node->right != null ){ $this->selectMax($node->right); }
  
  return $node; }
public function add2( $node,$value ){ if(!is_object($node)){ $node = new TreeBinarySearch(null); }
```
 if( $node->val == $value ){
     return $node;
 }

 if( $node->val == null ){
     $node->val = $value;
     $this->size++;
     return $node;
 }

 if( $node->val > $value){
      $node->left = $this->add2($node->left,$value);
 }

 if( $node->val < $value ){
      $node->right = $this->add2($node->right,$value);
 }

 return $node;  }
```
/**
- 前序遍历 */ public function selectPreorder($node,$level=1){ if( $node == null ){ return; }
  
  echo $this->deepShow($level); echo $node->val . “\n”;
  
  $this->selectPreorder($node->left,$level+1);
  
  $this->selectPreorder($node->right,$level+1); }
/**
- 前序遍历（栈） */ public function selectPreorderByStack($node){ //栈 $stack = []; array_push($stack,$node); while (!empty($stack)){
```
$cur = array_pop($stack);

echo $cur->val . "\n";


if( $cur->right ){
    $stack[] = $cur->right;
}

if( $cur->left ){
    $stack[] = $cur->left;
} }  }
```
/**
- 中序遍历 */ public function selectInorder($node,$level=1){ if( $node == null ){ return; }
  
  $this->selectInorder($node->left,$level+1);
  
  echo $this->deepShow($level); echo $node->val . “\n”;
  
  $this->selectInorder($node->right,$level+1); }
/**
- 中序遍历(栈) */ public function selectInorderByStack($node){
  
  $stack = [$node]; while( !empty($stack) ){
```
 $cur = array_pop($stack);

 if( $cur->left ){
     $stack[] = $cur->left;
 }else{
     echo $cur->val . "\n";
 }


 if( $cur->right ){
     $stack[] = $cur->right;
 }else{
     echo $cur->val . "\n";
 }
```
  }
}

/**
- 后序遍历 */ public function selectLastorder($node,$level=1){ if( $node == null ){ return; }
  
  $this->selectLastorder($node->right,$level+1);
  
  echo $this->deepShow($level); echo $node->val . “\n”;
  
  $this->selectLastorder($node->left,$level+1);
}

/**
- 树深度 */ protected function deepShow($deep){ while($deep–){ echo ‘–’; } }
/**
- 删除最小节点
- @param TreeBinarySearch $node */ public function deleteMin( $node ){ if( $node->left==null ){ $rightNode = $node->right; $node->right = null; $this->size–; return $rightNode; }
  
  $node->left = $this->deleteMin($node->left); return $node; }
/**
- 删除最大节点
- @param TreeBinarySearch $node */ public function deleteMax($node){ if( $node->right == null ){ $leftNode = $node->left; $node->left = null; $this->size–; return $leftNode; } $node->right = $this->deleteMax($node->right); return $node; }
/**
- 删除任意节点
- @param $node
- @param $value */ public function delete($value){ return $this->deleteByRecursion($this,$value); }
public function deleteByRecursion($node,$value){ if( $this->size==0 ) throw new \Exception(‘节点为空’);
```
 //空返回错误
 if( $node==null )
     return false;

 //找到节点
 if(  $node->val != $value ){
     //先从左节点找 再又节点  性能较差 //            return $this->deleteByRecursion($node->left,$value) or $this->deleteByRecursion($node->right,$value);
     //二分查找
     $node =  $this->select($value);
 }

 //目标节点左右节点为空 返回空
 if( $node->left==null && $node->right == null ){
     $node->val=null;
     $this->size--;
     return $node;
 }

 //右节点
 if( $node->right ){
     //获取右边最大值
     $nodeRightMin = $this->selectMin($node->right);

     //当前节点
     $node->val = $nodeRightMin->val;
     $node->right = $this->deleteMin($node->right);
 }else{
     //获取左节点最大值
     $nodeLeftMax = $this->selectMax($node->left);
     $node->val = $nodeLeftMax->val;
     $node->left = $this->deleteMax($node->left);
 }

 return $node;  }
```

} ```

WalkingSun

数据结构-树

树

二叉树

二分搜索树

添加新元素

遍历

删除操作

Search

Table of Contents